Slant Asymptote Lines: Example 2: Horizontal Hyperbola
2
About :
In this video I go over another example on Slant Asymptotes and this time look at the slant asymptote lines of a horizontal hyperbola, which is a hyperbola that extends outwards horizontally. The hyperbola x2/a2 – y2/b2 = 1 where a and b are constants has slant asymptote lines y = +/- (b/a)x. This is proven by applying the definition of slant asymptotes which I covered in my earlier video, and that is the limit as x approaches infinity of the difference between the function and a line approaches zero. In other words the function, in this case the hyperbola, approaches the asymptote lines. In proving this, I first rearrange the hyperbola to write it as y = f(x). But since the function involves square rooting a square, we get a two part function that can be either positive or negative, and thus to save time I combined all of the +/- terms (as well as the limit as x approaches +/- infinity) in just one limit formula. This was a shortcut on my part, but nonetheless the result is the same for this particular example as compared with doing it individually. I will be referencing this example on slant asymptotes for a horizontal hyperbola in my later videos, so make sure you watch this video and understand the derivation!
Download the notes in my video: https://1drv.ms/b/s!As32ynv0LoaIh5E1eR_74BRIMsvEmA
View video notes on the Hive blockchain: https://peakd.com/mathematics/@mes/slant-asymptote-lines-example-2-horizontal-hyperbola
Related Videos:
Slant Asymptote Lines: Example 1: Rational Function: https://youtu.be/FT5yNtPeBvg
Slant Asymptote Lines + Special Case: Rational Functions and Long Division: https://youtu.be/QX2nfi5JtQs
Hyperbola - Definition and derivation of the equation: x2/a2 - y2/b2 = 1: http://youtu.be/Y6iYC4VEAi0
Limits at Infinity: Horizontal Asymptotes: http://youtu.be/6pdgb09wRvI .
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
Like, Subscribe, Favorite, and Comment Below!
Follow us on:
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Gab: https://gab.ai/matheasysolutions
Minds: https://minds.com/matheasysolutions
Twitter: https://twitter.com/MathEasySolns
Facebook: https://fb.com/MathEasySolutions
LinkedIn: https://mes.fm/linkedin
Pinterest: https://pinterest.com/MathEasySolns
Instagram: https://instagram.com/MathEasySolutions
Email me: contact@mes.fm
Try our Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Try our Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
Tags :
Their limit for today is $0!






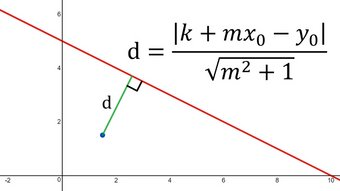


















Comments:
Reply:
To comment on this video please connect a HIVE account to your profile: Connect HIVE Account