Hyperbolic Functions: Catenary: Formula and Proof
9
About :
In this video I go over a really fascinating curve, and that is the catenary which is the shape formed by handing a heavy cable across two heights of equal heights. For example telephone cables and power lines hang according to this catenary shape. The word catenary stems from the Latin “catena” which means “chain”. While the curve “appears” to look like a parabola it is in fact not a parabolic shape, but rather a hyperbolic function, hyperbolic cosine (cosh) to be exact. The catenary formula is usually written as y = acosh(x/a) + c or y = cosh(ax)/a + c, whereas my calculus book uses the former.
The derivation involves some basic static equilibrium physics by first breaking up a segment of the chain and using a Free-Body Diagram to illustrate all of the forces at play. Summing up the horizontal and vertical components of the forces to ensure they sum up to zero (i.e. that the chain is static and not moving with an acceleration), we are able to obtain a differential equation for the curve. This equation includes the arc length of the chain segment, and thus we can apply the formula arc length, and a whole lot of tedious algebra later to finally obtain the hyperbolic catenary function!
I also go over a brief history lesson on the catenary and show how the likes of Galileo, Huygens, Leibniz, and Bernoulli brothers Jacob and Johann were involved in a rigorous mathematical battle to try to determine the formula of the catenary, which shocked Galileo’s assumption of it being a parabola. The catenary has some very interesting properties, and the fact that it is formed by simply holding a heavy cable up by two heights helps explain how it has a very low center of gravity and small potential energy. I may investigate more into the catenary so stay tuned!
Download the notes in my video: https://1drv.ms/b/s!As32ynv0LoaIhvofvd_G4uxmjT0IjQ
View video notes on the Hive blockchain: https://peakd.com/mathematics/@mes/vcsmh-video-notes-hyperbolic-functions-catenary-formula-and-proof
Related Videos:
Hyperbolic Functions - tanh(x), sinh(x), cosh(x) - Introduction: http://youtu.be/EmJKuQBEdlc
Applications of Integrals: Arc Length Proof: https://youtu.be/2rb4H_rmgxg .
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
Like, Subscribe, Favorite, and Comment Below!
Follow us on:
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Gab: https://gab.ai/matheasysolutions
Minds: https://minds.com/matheasysolutions
Twitter: https://twitter.com/MathEasySolns
Facebook: https://fb.com/MathEasySolutions
LinkedIn: https://mes.fm/linkedin
Pinterest: https://pinterest.com/MathEasySolns
Instagram: https://instagram.com/MathEasySolutions
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
Tags :
Their limit for today is $0!


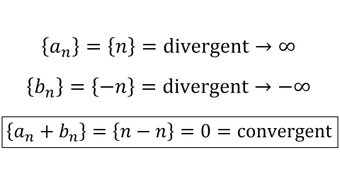
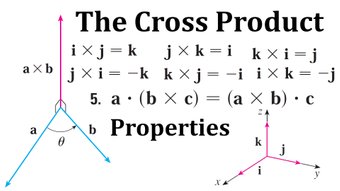

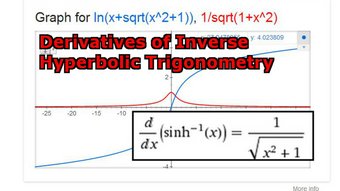





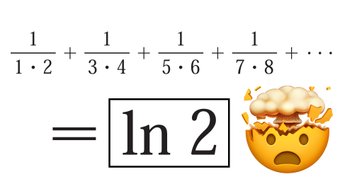















Comments:
Reply:
To comment on this video please connect a HIVE account to your profile: Connect HIVE Account