Conic Sections: Hyperbola: Definition and Formula

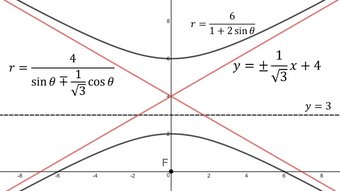
In this video I go over further into Conic Sections and this time go over the definition of a Hyperbola and derive its resulting formula. I had gone over this derivation several years ago but I have decided to revisit it to be better tie into the Conic Sections video series I have recently been making, as well as to go over it in more detail. The Hyperbola is defined as the set of points on a plane with the property that the difference in the distances from each point to two fixed points (known as the foci) is a constant. Using this definition for the foci on the x-axis, I first show that the difference is equal to +/- 2a because this is the difference when the Hyperbola is also on the x-axis, at either of the two points known as the vertices, and is thus defined as constant for Hyperbolas.

The derivation for the hyperbola is very similar to that for the ellipse, which I covered in my earlier video, and involves using the Pythagorean Theorem for the distances and combined with a lot of algebra to simplify the resulting formulation. After some careful algebra, I show that we can eventually write the hyperbola as x²/a² – y²/b² = 1 and where b² = c² – a². The resulting graph of the hyperbola consists of two branches that extend outwards approaching the slant asymptote lines, which I covered in my last two videos, and are y = +/ (b/a)x. This is known as a Horizontal Hyperbola, but we can switch up the x and y terms to get a Vertical Hyperbola y²/a² – x²/b² = 1 and with slant asymptotes y = +/- (a/b)x. This is a very extensive video covering the definition and derivation of Hyperbolas so make sure to watch this video!

Download the notes in my video: https://1drv.ms/b/s!As32ynv0LoaIh5FP9bXo4PFSmGkJZw

View video notes on the Hive blockchain: https://peakd.com/mathematics/@mes/conic-sections-hyperbola-definition-and-formula

Related Videos:

Conic Sections: Parabolas: Definition and Formula: https://youtu.be/kCJjXuuIqbE
Conic Sections: Ellipses: Definition and Derivation of Formula (Including Circles): https://youtu.be/9dETsJ2tz_M
Slant Asymptote Lines: Example 2: Horizontal Hyperbola: https://youtu.be/XSudAYmWJ-M
Slant Asymptote Lines: Example 3: Vertical Hyperbola: https://youtu.be/oFYvWFhcTwI
Hyperbola - Definition and derivation of the equation: x²/a² - y²/b² = 1: http://youtu.be/Y6iYC4VEAi0 .

SUBSCRIBE via EMAIL: https://mes.fm/subscribe

DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate

Like, Subscribe, Favorite, and Comment Below!

Follow us on:

Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Gab: https://gab.ai/matheasysolutions
Minds: https://minds.com/matheasysolutions
Twitter: https://twitter.com/MathEasySolns
Facebook: https://fb.com/MathEasySolutions
LinkedIn: https://mes.fm/linkedin
Pinterest: https://pinterest.com/MathEasySolns
Instagram: https://instagram.com/MathEasySolutions
Email me: contact@mes.fm

Try our Free Calculators: https://mes.fm/calculators

BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm

Try our Free Online Tools: https://mes.fm/tools

iPhone and Android Apps: https://mes.fm/mobile-apps