Conics in Polar Coordinates: Unified Theorem: Hyperbola Proof

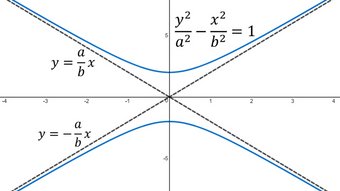
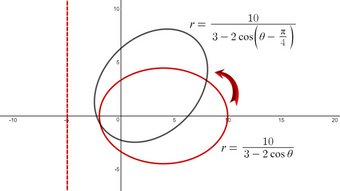
In this video I go over further into the Unified the Theorem for Conics and this time prove it is applicable for hyperbolas. Recall that the theorem states that a conic is formed when the ratio of the distance to the focus divided by the distance to the directrix is a constant e, called the eccentricity. In my earlier videos I proved the case for parabolas (e = 1) and ellipses (e is less than 1), and in this video I prove the case for when e is greater than 1, i.e. for hyperbolas. But to save time I carry off from the proof of ellipses in which I first derived a formula for the conic for the general case of e is not equal to 1. The resulting formula in Cartesian or Rectangular coordinates looks very much like that for ellipses and hyperbolas, but the different values of e decides which conic is described. For the case that e is greater than 1, I show that indeed the unified theorem describes a hyperbola, and in fact it is a shifted horizontally shifted horizontal hyperbola. And just like for the ellipses case, the focus defined by the unified theorem is the exact same as that defined by the conventional theorem, albeit having two foci.

This is a very important video to understand how different theorems can describe the same curve but for better or worse across different coordinate systems. I will be going over some examples in later videos to better illustrate this theorem and its very simple formulation in polar coordinates so stay tuned!

Download the notes in my video: https://1drv.ms/b/s!As32ynv0LoaIh5pCF992AdJKQ8h1Dw

View video notes on the Hive blockchain: https://peakd.com/mathematics/@mes/conics-in-polar-coordinates-unified-theorem-hyperbola-proof

Related Videos:

Conics in Polar Coordinates Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0H4OJpJ2gslXVLT8mP-SgJP
Conic Sections Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0FEUsuxP3KS5DRbidSSGBPL
Polar Coordinates Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0HUFiPLsYw5_Ljd5riOUzjP
Conics in Polar Coordinates: Unified Theorem: Ellipse Proof:

SUBSCRIBE via EMAIL: https://mes.fm/subscribe

DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate

Like, Subscribe, Favorite, and Comment Below!

Follow us on:

Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Gab: https://gab.ai/matheasysolutions
Minds: https://minds.com/matheasysolutions
Twitter: https://twitter.com/MathEasySolns
Facebook: https://fb.com/MathEasySolutions
LinkedIn: https://mes.fm/linkedin
Pinterest: https://pinterest.com/MathEasySolns
Instagram: https://instagram.com/MathEasySolutions
Email me: contact@mes.fm

Try our Free Calculators: https://mes.fm/calculators

BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm

Try our Free Online Tools: https://mes.fm/tools

iPhone and Android Apps: https://mes.fm/mobile-apps