Infinite Sequences and Series: Kummer’s Test, Raabe’s Test, and Convergence of Binomial Series
7
About :
In this video I go over more advanced tests for convergence in order to determine the convergence or divergence of the Binomial Series at the endpoints. In particular, I first derive Kummer’s Test, which is a generalization of both the Ratio Test, covered in my earlier video, and Raabe’s Test, which I cover in this video. I also show that Raabe’s Test is essentially a test that compares series to the p-series, which I had covered before.
In my earlier video, I had covered the Binomial Series and showed using the Ratio Test that the radius of convergence was less than 1 but the test was inconclusive at the endpoints. This is where I use Raabe’s Test to overcome the shortcomings of the Ratio Test and show that at the endpoints, the Binomial Series may converge or diverge depending on the value of k. This is a pretty epic and extensive proof video, and likely far more thorough than any other proof found online, so make sure to watch it!
Note that Kummer’s Test was first obtained by German mathematician Ernst Eduard Kummer, while Raabe’s Test was obtained by Swiss mathematician Joseph Ludwig Raabe, and both during the mid-1800s.
Also note, that I obtained the proofs for Kummer’s Test and Raabe’s Test from a paper by Sarah Fix from Whitman College, USA. As for the Binomial Series proof, I used mainly the lecture PDF by John Labute from McGill University, Canada.
The topics covered in this video are listed below with their time stamps.
- @ 1:29 - Topics to Cover
- @ 3:21 - Recap on the Ratio Test for Convergence
- @ 5:18 - Advanced Tests for Convergence
- @ 6:06 - Kummer's Test
- @ 36:02 - Ratio Test is Kummer's Test with Bn = 1
- @ 43:07 - Note on Kummer's Test
- @ 43:38 - Raabe's Test: Kummer's Test with Bn = n
- @ 51:45 - Raabe's Test Compares Series to the p-Series
- @ 1:02:05 - Corollary of Raabe's Test
- @ 1:23:01 - Note on Raabe's Test and Kummer's Test
- @ 6:06 - Kummer's Test
- @ 1:24:04 - Recap on Power Series
- @ 1:26:40 - Taylor and Maclaurin Series
- @ 1:27:32 - Recap on the Binomial Theorem
- @ 1:29:59 - Recap on the Binomial Series
- @ 1:32:32 - Convergence at the Endpoints Depends on the Value of k
- @ 1:34:48 - Important Note on the Binomial Coefficients
- @ 1:36:43 - Convergence of the Binomial Series
- @ 1:44:58 - Endpoint x = -1: Using Raabe's Test
- Converges when k is greater than 0
- Diverges when k is less than 0
- @ 2:01:43 - Endpoint x = 1: Alternating Series
- @ 2:07:37 - Using Raabe's Test: Absolute Convergence when k is greater than 0
- @ 2:12:34 - Using Alternating Series Test: Converges when k is between 0 and -1
- @ 2:42:53 - Pi Production Notation for Factorials
- @ 2:48:14 - Using Comparison Test: Diverges when k ≤ -1
- @ 2:58:30 - Can Also Use the Test for Divergence
- @ 2:59:12 - Trivial Case k = 0: Converges for all x
- @ 2:59:29 - Summary
- @ 1:44:58 - Endpoint x = -1: Using Raabe's Test
Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIiL4occLuFG9lN_2stg?e=jdv8Up
View video notes on the Hive blockchain: https://peakd.com/hive-128780/@mes/kummer-s-test-raabe-s-test-and-convergence-of-binomial-series
Related Videos:
Sequences and Series Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EXHAJ3vRg0T_kKEyPah1Lz
Infinite Sequences and Series: Power Series: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-power-series
Infinite Sequences and Series: Representations of Functions as Power Series: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series
Infinite Sequences and Series: Taylor and Maclaurin Series: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
Infinite Sequences and Series: The Comparison Tests: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests
Infinite Sequences and Series: Alternating Tests: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-alternating-tests
Infinite Sequences and Series: Strategy for Testing Series: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-strategy-for-testing-series .
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
Like, Subscribe, Favorite, and Comment Below!
Follow us on:
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Gab: https://gab.ai/matheasysolutions
Minds: https://minds.com/matheasysolutions
Twitter: https://twitter.com/MathEasySolns
Facebook: https://fb.com/MathEasySolutions
LinkedIn: https://mes.fm/linkedin
Pinterest: https://pinterest.com/MathEasySolns
Instagram: https://instagram.com/MathEasySolutions
Email me: contact@mes.fm
Try our Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Try our Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
Tags :
Their limit for today is $0!















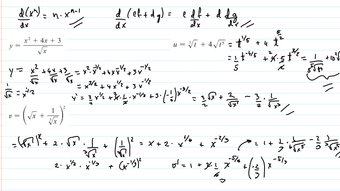
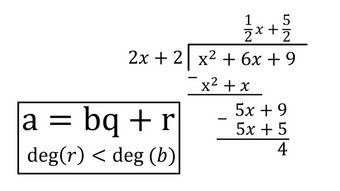





Comments:
Reply:
To comment on this video please connect a HIVE account to your profile: Connect HIVE Account